We’re picking up where we left off (here’s part 1), with two trees of similar stature, though each with vastly different numbers of leaves. Our sugar maple comes in at 1,060 leaves, while our striped maple has just 306. At first glance, this seems like a significant difference, but striped maple leaves are gigantic while sugar maples, well, aren’t. So we need a better way to compare these two numbers. Here I want to figure out two things: first which tree takes up more space in the canopy and second, which tree has more photosynthetic surface area. And next time we’ll look at some of the differences in the life history strategies of striped vs sugar maple.
Size of the crown
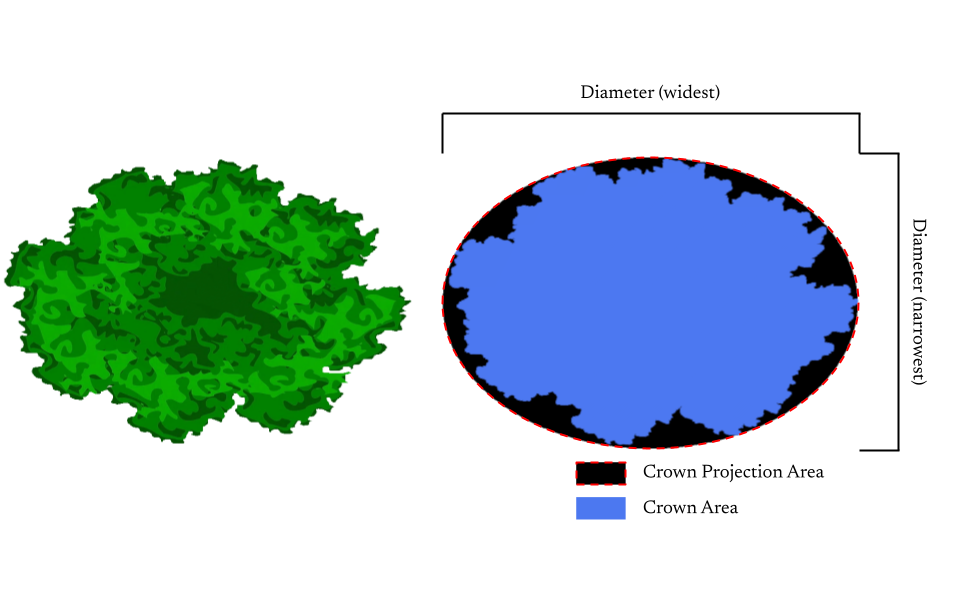
There are two measurements that can help us understand how much space a tree takes up in the canopy. The first, called crown area, is a rather precise measurement of the total area that a tree’s crown covers on the ground below. This would be similar to the shaded area on the forest floor from the shadow cast down by the leaves if the sun was directly overhead.
The second is the crown projection area (CPA), a measurement of how much space the outer edges of the tree’s crown takes up in the forest and includes all the negative space between leaves and branches. It is measured by drawing a circle or oval that encompasses the crown area.
As tree crowns aren’t perfect circles, it’s a bit tricky to get an exact measurement of CPA. There are a few methods that foresters use to get at a precise answer, and I’m sure they’d argue endlessly over which method is best. But I don’t need precise, so I just took the average crown spread at the widest and narrowest parts of the canopy for the two trees and assumed the crowns were ellipses.
Calculating Crown Projection Area (CPA)
To find the area of an ellipse, us use the following formula:
Area = π * a * b (where a = radius at widest point and b = radius at the narrowest point)
Our striped maple was 86″ across at the narrowest and 126″ at the widest (it was growing up against another tree which made it more elliptical). The sugar maple was more circular at 147″ at the widest and 140″ at the narrowest. For crown projection area we get:
CPA Striped maple = π * (86/2)” * (126/2)” = 8,510 in² or 59.1 ft²
CPA Sugar maple = π * (140/2)” * (146/2)” = 16,163 in² or 112.2 ft²
So despite being roughly the same height and diameter, the two trees had dramatically different crown spreads, and the sugar maple had double the CPA as the striped maple. This will obviously impact the total photosynthetic area for each tree.
But the crown of a tree isn’t just made up of one solid sheet of leaves covering the whole crown area like a bunch of leaves pasted onto an umbrella. The leaves are arranged along multiple layers of branches. Some leaves have gaps between them while others overlap, so CPA doesn’t give us the full picture.
To get a better sense of how much total surface area the leaves on a tree cover, I needed to find the average size of the leaves on each tree and then multiply this by the total number of leaves. I could then compare this number (the leaf surface area) to the CPA for each tree and get a sense of how much photosynthetic space each tree utilizes within its crown area. This would be particularly interesting as we’d be comparing a shade tolerant understory tree (striped maple) with a shade tolerant canopy tree (sugar maple).
To do this I used a really fun (and free) tool that digitally measures the area of an irregular polygon (link). The process is a bit of a black box to me, but essentially, you take a photo of an object alongside some reference for scale (like a ruler) and then the program calculates the total area of the leaf based off the scale that you provide (here’s a tutorial video on the process: link). Easy peasy.
Since the leaves vary greatly in size, I wanted a random sample of leaves on each tree. I used kids in the summer camp to help choose 10 random leaves selected from both trees (I had them choose random numbers to select the first branch point on the trunk, then another kid to choose the next branch point and so on). It was fun.
The raw data
After taking photos of all the leaves, I then used ImageJ to calculate the area of each leaf:
| Leaf # | Surface area of sugar maple leaves (in²) |
Surface area of striped maple leaves (in²) |
| 1 | 1.8 | 10.1 |
| 2 | 6.3 | 17.5 |
| 3 | 7.2 | 33.9 |
| 4 | 7.6 | 33.9 |
| 5 | 9.0 | 41.0 |
| 6 | 9.5 | 45.3 |
| 7 | 9.9 | 47.7 |
| 8 | 10.3 | 48.8 |
| 9 | 12.5 | 61.1 |
| 10 | 17.9 | 89.4 |
| Avg |
9.2 |
42.9 |
It’s obvious from looking at the leaves, that striped maple leaves are significantly larger, but here we quantify it, with the leaves roughly 4.5x larger!
And now that we have the average leave size, it is then quite easy to estimate the total surface area covered by all the leaves on the tree and compare this to the CPA of the crown (again, the space the tree takes up in the canopy):
Leaf Surface Area Sugar maple = 1,060 leaves * 9.2 in²/leaf (avg surface area of a leaf) = 9,752 in² = 67.7 ft² (compare to a CPA of just 19.5 ft²)
Leaf Surface Area Striped maple = 306 leaves * 42.9 in²/leaf (avg surface area of a leaf) = 13,127.4 in² = 91.1 ft² (compare to a CPA of just 35.8 ft²)
In the next issue I’ll look at some of the possible explanations behind all these numbers.